- v50 information can now be added to pages in the main namespace. v0.47 information can still be found in the DF2014 namespace. See here for more details on the new versioning policy.
- Use this page to report any issues related to the migration.
Difference between revisions of "User:BaronW"
| Line 4: | Line 4: | ||
I have made a calculator. | I have made a calculator. | ||
It can add, subtract, divide and multiply. | It can add, subtract, divide and multiply. | ||
| − | It can take inputs of up to 999 and give answers of up to 999999 | + | It can take inputs of up to 999 and give answers of up to 999999 or 999.999. |
[[File:7x191.PNG]] | [[File:7x191.PNG]] | ||
| Line 26: | Line 26: | ||
[[File:Addition cell 1&2.GIF]] | [[File:Addition cell 1&2.GIF]] | ||
<br /> | <br /> | ||
| − | Each cell is designed to add a two or three binary digits together. The first cell adds 2 digits (that is one from each of the input numbers). When you add 2 binary digits together there are 4 possible ways for them to combine and 3 possible outcomes (0+0=0 0+1=1 1+0=1 1+1=10), however an outcome of 0 does not change the answer so you do not need to build it (In the addition engine I did build it but i later disconnected it). So each input gets a line of mechanisms, A line and B line, since there are 3 important ways of combining the inputs each line has 3 mechanisms. levers are connected to some mechanisms so they can be 'flipped' and thereby each row made to represent one possible outcome. A screw-pump is then connected to each outcome which triggers a pressure-plate which triggers either the outcome or the C line of the next cell. | + | Each cell is designed to add a two or three binary digits together. The first cell adds 2 digits (that is one from each of the input numbers). When you add 2 binary digits together there are 4 possible ways for them to combine and 3 possible outcomes (0+0=0, 0+1=1, 1+0=1, 1+1=10), however an outcome of 0 does not change the answer so you do not need to build it (In the addition engine I did build it but i later disconnected it). So each input gets a line of mechanisms, A line and B line, since there are 3 important ways of combining the inputs each line has 3 mechanisms. levers are connected to some mechanisms so they can be 'flipped' and thereby each row made to represent one possible outcome. A screw-pump is then connected to each outcome which triggers a pressure-plate which triggers either the outcome or the C line of the next cell. |
<br /> The second and all subsequent cells need to add a C line that is triggered when the answer of the previous cell is 10 or 11. And so there becomes 8 (7 important) ways for the digits to combine and 4 possible outcomes (3 important). But an all other ways cell 2-10 is the same as cell 1.<br /> | <br /> The second and all subsequent cells need to add a C line that is triggered when the answer of the previous cell is 10 or 11. And so there becomes 8 (7 important) ways for the digits to combine and 4 possible outcomes (3 important). But an all other ways cell 2-10 is the same as cell 1.<br /> | ||
[[File:Addition cell b 1&2.GIF]]<br /> | [[File:Addition cell b 1&2.GIF]]<br /> | ||
And the whole addition engine looks like this<br /> | And the whole addition engine looks like this<br /> | ||
[[File:Addition.PNG]] | [[File:Addition.PNG]] | ||
| + | |||
| + | == Subtraction (binary)== | ||
| + | |||
| + | Subtraction works much the same as addition except that the A-line input is positive and the B-line and C-line inputs are negative. So the possible outcomes are (from a 3 line input) (in the order I put them in the engine) 1-0-0=01, 1-1-1=-11, 0-0-1=-11, 0-1-0=-11, 0-1-1=-10, 1-0-1=0, 1-1-0=0, 0-0-0=0. This has the advantage that there are 3 irrelevant outcomes in each cell so you only need to build 5 rows in each cell.<br /> | ||
| + | Subtraction engine.<br /> | ||
| + | [[File:Subtraction main.PNG]]<br /> | ||
| + | The one difficulty in subtraction is that the engine has no idea what a negative number is, so if you want the calculator to be able to give a negative response you need to teach it. My solution (possibly massively overcomplicated) was to build a which number is larger engine and then tell the subtraction engine to subtract the smaller number from the larger. A 'which number is larger' engine is not easy. It is presented with 2 10 digit binary numbers A1-A10 & B1-B10 then asks: does 'A1=1 and B1=0' or does 'B1=1 n and A1=0' if the answer is yes to either, that will mean that one number is larger than the other. It will then send power to a set of screw-pumps that will then tell the main engine which number to subtract from which. If the answer is no to both then it will ask does 'A2=1 and B2=0' or does 'B2=1 n and A2=0', this repeats until it decided which number is larger or that they are the same.<br /> | ||
| + | The engine looks like this- the main bit is in the botem right.<br /> | ||
| + | [[File:Which number is larger.PNG]] | ||
Revision as of 13:29, 12 April 2010
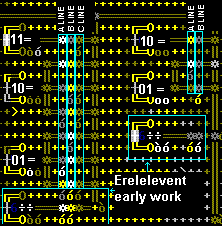
The Almighty Dwarven Calculator
What can you do with 75,368 mechanisms and 40,000 power?
I have made a calculator.
It can add, subtract, divide and multiply.
It can take inputs of up to 999 and give answers of up to 999999 or 999.999.
How to use
The in control house (shown above calculating 7x191) there 6 groups of leavers each group corresponds to an input number, and each lever within a group corresponds to a number (in the same pattern as on a cell phone). Once the leavers that represent the desired numbers have been pulled (only one lever per group or things will go wrong).
Then select the desired function (+ * - /) by pulling the indicated lever. The selected function will be displayed.
Then select pull the equals lever, go and make a cup of tea, some soup perhaps compose a sonnet (it takes a long time even for simple equations).
Your answer will then be displayed in glorious digital numbers.
How it works
Addition (binary)
In essence what you need to do to make any computer work is to brake the job down to its simplest possible functions. To that end all actual computation is don in binary.
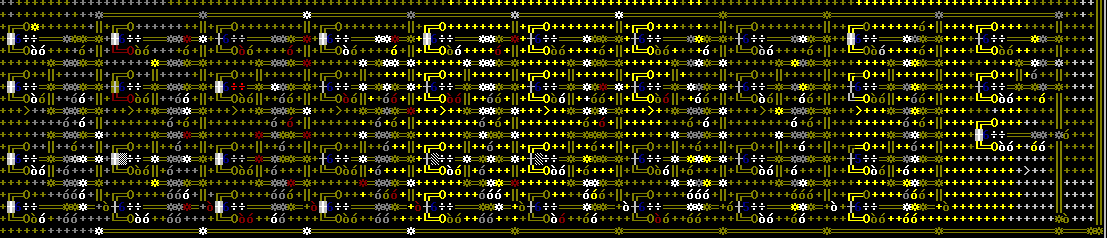
This is the first 2 cells from the addition engine.

Each cell is designed to add a two or three binary digits together. The first cell adds 2 digits (that is one from each of the input numbers). When you add 2 binary digits together there are 4 possible ways for them to combine and 3 possible outcomes (0+0=0, 0+1=1, 1+0=1, 1+1=10), however an outcome of 0 does not change the answer so you do not need to build it (In the addition engine I did build it but i later disconnected it). So each input gets a line of mechanisms, A line and B line, since there are 3 important ways of combining the inputs each line has 3 mechanisms. levers are connected to some mechanisms so they can be 'flipped' and thereby each row made to represent one possible outcome. A screw-pump is then connected to each outcome which triggers a pressure-plate which triggers either the outcome or the C line of the next cell.
The second and all subsequent cells need to add a C line that is triggered when the answer of the previous cell is 10 or 11. And so there becomes 8 (7 important) ways for the digits to combine and 4 possible outcomes (3 important). But an all other ways cell 2-10 is the same as cell 1.
And the whole addition engine looks like this
Subtraction (binary)
Subtraction works much the same as addition except that the A-line input is positive and the B-line and C-line inputs are negative. So the possible outcomes are (from a 3 line input) (in the order I put them in the engine) 1-0-0=01, 1-1-1=-11, 0-0-1=-11, 0-1-0=-11, 0-1-1=-10, 1-0-1=0, 1-1-0=0, 0-0-0=0. This has the advantage that there are 3 irrelevant outcomes in each cell so you only need to build 5 rows in each cell.
Subtraction engine.
The one difficulty in subtraction is that the engine has no idea what a negative number is, so if you want the calculator to be able to give a negative response you need to teach it. My solution (possibly massively overcomplicated) was to build a which number is larger engine and then tell the subtraction engine to subtract the smaller number from the larger. A 'which number is larger' engine is not easy. It is presented with 2 10 digit binary numbers A1-A10 & B1-B10 then asks: does 'A1=1 and B1=0' or does 'B1=1 n and A1=0' if the answer is yes to either, that will mean that one number is larger than the other. It will then send power to a set of screw-pumps that will then tell the main engine which number to subtract from which. If the answer is no to both then it will ask does 'A2=1 and B2=0' or does 'B2=1 n and A2=0', this repeats until it decided which number is larger or that they are the same.
The engine looks like this- the main bit is in the botem right.