v50 Steam/Premium information for editors
  • v50 information can now be added to pages in the main namespace. v0.47 information can still be found in the DF2014 namespace. See here for more details on the new versioning policy.
  • Use this page to report any issues related to the migration.
This notice may be cached—the current version can be found here.

Difference between revisions of "40d:Fluid logic"

From Dwarf Fortress Wiki
Jump to navigation Jump to search
m (Images are fine; this is not a standard topic.)
Line 1: Line 1:
−
 
 
Fluid logic is a form of [[computing]] which uses a fluid (generally [[water]]) controlled by various means, to trigger [[pressure plate]]s and hopefully accomplish some desirable result.
 
Fluid logic is a form of [[computing]] which uses a fluid (generally [[water]]) controlled by various means, to trigger [[pressure plate]]s and hopefully accomplish some desirable result.
  
Line 17: Line 16:
 
[[File:Inverter.gif|thumb]]
 
[[File:Inverter.gif|thumb]]
 
Perhaps the closest to utilizing water as a stand-in for electricity, transmission gate logic can be accomplished by simply having an infinite water source in place of all +Vs, and infinite drainage for all grounds.  Simple floodgates behave as standard transmission gates, while bridges are inverted gates.  However, unlike the other forms of fluid logic, but like a real world electrical circuit, a dedicated inverter is required, which must be hooked up to +V and ground.
 
Perhaps the closest to utilizing water as a stand-in for electricity, transmission gate logic can be accomplished by simply having an infinite water source in place of all +Vs, and infinite drainage for all grounds.  Simple floodgates behave as standard transmission gates, while bridges are inverted gates.  However, unlike the other forms of fluid logic, but like a real world electrical circuit, a dedicated inverter is required, which must be hooked up to +V and ground.
 +
 +
==Advanced CMOS Gates==
 +
This type of logic uses the same concept as real CMOS circuits do, which causes them to minimalize power (in this case, water) consumption. The idea is that water should only flow when there is a state change.
 +
 +
===Basic Design===
 +
Let's say we want to evaluate the logical expression ''f''. It can be a simple '''and''' or '''or''' gate, or anything more complicated. Follow the following scheme:
 +
 +
{| style="border-spacing: 0"
 +
|{{H2O}}
 +
|{{H2O}}
 +
|{{H2O}}
 +
|-
 +
|{{RTF|╗}}
 +
|{{RTF|A}}
 +
|{{RTF|╔}}
 +
|-
 +
|{{RTF|║}}
 +
|{{RT0|^|#808}}
 +
|{{RTF|║}}
 +
|-
 +
|{{RTF|║}}
 +
|{{RTF|B}}
 +
|{{RTF|║}}
 +
|-
 +
|{{RTF|║}}
 +
|{{RTF|#}}
 +
|{{RTF|║}}
 +
|}
 +
 +
Here, {{Tile|A|#FFF|#000}} is a set of floodgates and/or drawbridges that let water flow exactly when ''f'' evaluates to true, {{Tile|B|#FFF|#000}} is the same except that it lets water flow when ''f'' evaluates to false, {{Tile|^|#808|#000}} is a pressure plate set to activate on water levels 4-7, and {{Tile|#|#FFF|#000}} is the drain.
 +
 +
===Examples===
 +
In the following examples, {{Tile|X|#000|#888}} is a floodgate, and {{Tile|╬|#FFF|#000}} is a drawbridge. Red ones are connected to input A, green ones to input B and blue ones to input C.
 +
 +
====NOT====
 +
{| style="border-spacing: 0"
 +
|{{H2O}}
 +
|{{H2O}}
 +
|{{H2O}}
 +
|-
 +
|{{RTF|╗}}
 +
|{{RT|╬|#F00|#000}}
 +
|{{RTF|╔}}
 +
|-
 +
|{{RTF|║}}
 +
|{{RT0|^|#808}}
 +
|{{RTF|║}}
 +
|-
 +
|{{RTF|║}}
 +
|{{RT|X|#FFF|#800}}
 +
|{{RTF|║}}
 +
|-
 +
|{{RTF|║}}
 +
|{{RTF|#}}
 +
|{{RTF|║}}
 +
|}
 +
 +
====AND====
 +
{| style="border-spacing: 0"
 +
|{{H2O}}
 +
|{{H2O}}
 +
|{{H2O}}
 +
|{{H2O}}
 +
|-
 +
|{{RTF|╗}}
 +
|{{RT|X|#FFF|#800}}
 +
|{{RTF|╔}}
 +
|{{RTF|═}}
 +
|-
 +
|{{RTF|║}}
 +
|{{RT|X|#FFF|#080}}
 +
|{{RTF|║}}
 +
|{{000}}
 +
|-
 +
|{{RTF|║}}
 +
|{{RT0|^|#808}}
 +
|{{RTF|╚}}
 +
|{{RTF|╗}}
 +
|-
 +
|{{RTF|║}}
 +
|{{000}}
 +
|{{000}}
 +
|{{RTF|║}}
 +
|-
 +
|{{RTF|║}}
 +
|{{RT|╬|#F00|#000}}
 +
|{{RT|╬|#0F0|#000}}
 +
|{{RTF|║}}
 +
|-
 +
|{{RTF|║}}
 +
|{{RTF|#}}
 +
|{{RTF|#}}
 +
|{{RTF|║}}
 +
|}
 +
 +
====OR====
 +
{| style="border-spacing: 0"
 +
|{{H2O}}
 +
|{{H2O}}
 +
|{{H2O}}
 +
|{{H2O}}
 +
|-
 +
|{{RTF|╗}}
 +
|{{RT|X|#FFF|#800}}
 +
|{{RT|X|#FFF|#080}}
 +
|{{RTF|╔}}
 +
|-
 +
|{{RTF|║}}
 +
|{{000}}
 +
|{{000}}
 +
|{{RTF|║}}
 +
|-
 +
|{{RTF|║}}
 +
|{{RT0|^|#808}}
 +
|{{RTF|╔}}
 +
|{{RTF|╝}}
 +
|-
 +
|{{RTF|║}}
 +
|{{RT|╬|#F00|#000}}
 +
|{{RTF|║}}
 +
|{{000}}
 +
|-
 +
|{{RTF|║}}
 +
|{{RT|╬|#0F0|#000}}
 +
|{{RTF|║}}
 +
|{{000}}
 +
|-
 +
|{{RTF|║}}
 +
|{{RTF|#}}
 +
|{{RTF|║}}
 +
|{{000}}
 +
|}
 +
 +
====XOR====
 +
This is not as straightforward as the previous ones. The ''true'' expression is the following: (A '''and not''' B) '''or''' ('''not''' A '''and''' B). The ''false'' expression: (A '''and''' B) '''or''' ('''not''' A '''and not''' B).
 +
 +
So the gates look like the following:
 +
 +
{| style="border-spacing: 0"
 +
|{{H2O}}
 +
|{{H2O}}
 +
|{{H2O}}
 +
|{{H2O}}
 +
|{{H2O}}
 +
|-
 +
|{{RTF|╗}}
 +
|{{RT|X|#FFF|#800}}
 +
|{{RTF|║}}
 +
|{{RT|X|#FFF|#080}}
 +
|{{RTF|╔}}
 +
|-
 +
|{{RTF|║}}
 +
|{{RT|╬|#0F0|#000}}
 +
|{{RTF|║}}
 +
|{{RT|╬|#F00|#000}}
 +
|{{RTF|║}}
 +
|-
 +
|{{RTF|║}}
 +
|{{000}}
 +
|{{RT0|^|#808}}
 +
|{{000}}
 +
|{{RTF|║}}
 +
|-
 +
|{{RTF|║}}
 +
|{{RT|╬|#F00|#000}}
 +
|{{RTF|║}}
 +
|{{RT|X|#FFF|#800}}
 +
|{{RTF|║}}
 +
|-
 +
|{{RTF|║}}
 +
|{{RT|╬|#0F0|#000}}
 +
|{{RTF|║}}
 +
|{{RT|X|#FFF|#080}}
 +
|{{RTF|║}}
 +
|-
 +
|{{RTF|║}}
 +
|{{RTF|#}}
 +
|{{RTF|║}}
 +
|{{RTF|#}}
 +
|{{RTF|║}}
 +
|}
 +
 +
===Advantages And Disadvantages===
 +
The basic advantage of this design is that it uses much less water than infinite flow gates. A river is enough to supply even the more complex systems, maybe with an added reservoir to neutralise flow irregularities. Similarly, for the drain, it is enough to excavate a cavern where the water can evaporate.
 +
 +
The disadvantage is that it requires much more resources and time to construct, especially more mechanisms. And more planning, since floodgates tend to block paths when constructed.
  
 
[[Category:Constructions]]
 
[[Category:Constructions]]

Revision as of 12:45, 30 November 2009

Fluid logic is a form of computing which uses a fluid (generally water) controlled by various means, to trigger pressure plates and hopefully accomplish some desirable result.

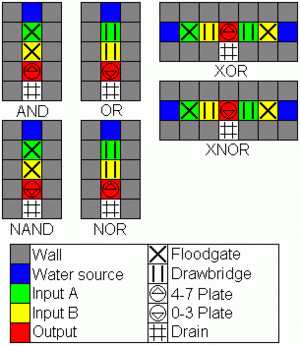
Infinite Flow Gates

Logic1.gif

These logic gates are relatively simple and cheap to make, but require an infinite amount of water and infinite drainage to operate (alternatively a power-hungry pump-circuit). Credit goes to numerous forum members for refining these designs.

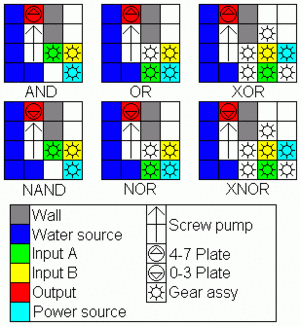
Mechanical-Fluid Gates

Logic2.gif

The water sources in these diagrams are located 1 z-level below the pumps and gear assemblies.

These gate designs have the advantage of destroying no water and requiring no drainage off the map, making them suitable for maps where infinite water and/or drainage may be a problem. The only fluid lost will be to evaporation. However, there are a number of disadvantages. They require significantly more materials and time to make, they require power, and a flood could have disasterous consequences, as it would cover all the plates at once.

For the XOR-Gate it is assumed that the gear is powered by a windmill on a map with strong wind (40 power). If both gears are active the XOR-Gate would need more than 40 power and will stop working. If you use a different source of power - a waterwheel with axles or combined windmills 20 power each - you´ll have to add or remove some gears or axles to calibrate it.

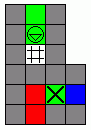
CMOS Transmission Gate and Inverter Logic

Inverter.gif

Perhaps the closest to utilizing water as a stand-in for electricity, transmission gate logic can be accomplished by simply having an infinite water source in place of all +Vs, and infinite drainage for all grounds. Simple floodgates behave as standard transmission gates, while bridges are inverted gates. However, unlike the other forms of fluid logic, but like a real world electrical circuit, a dedicated inverter is required, which must be hooked up to +V and ground.

Advanced CMOS Gates

This type of logic uses the same concept as real CMOS circuits do, which causes them to minimalize power (in this case, water) consumption. The idea is that water should only flow when there is a state change.

Basic Design

Let's say we want to evaluate the logical expression f. It can be a simple and or or gate, or anything more complicated. Follow the following scheme:

≈ ≈ ≈
╗ A ╔
║ ^ ║
║ B ║
║ # ║

Here, A is a set of floodgates and/or drawbridges that let water flow exactly when f evaluates to true, B is the same except that it lets water flow when f evaluates to false, ^ is a pressure plate set to activate on water levels 4-7, and # is the drain.

Examples

In the following examples, X is a floodgate, and ╬ is a drawbridge. Red ones are connected to input A, green ones to input B and blue ones to input C.

NOT

≈ ≈ ≈
╗ ╬ ╔
║ ^ ║
║ X ║
║ # ║

AND

≈ ≈ ≈ ≈
╗ X ╔ ═
║ X ║ █
║ ^ ╚ ╗
║ █ █ ║
║ ╬ ╬ ║
║ # # ║

OR

≈ ≈ ≈ ≈
╗ X X ╔
║ █ █ ║
║ ^ ╔ ╝
║ ╬ ║ █
║ ╬ ║ █
║ # ║ █

XOR

This is not as straightforward as the previous ones. The true expression is the following: (A and not B) or (not A and B). The false expression: (A and B) or (not A and not B).

So the gates look like the following:

≈ ≈ ≈ ≈ ≈
╗ X ║ X ╔
║ ╬ ║ ╬ ║
║ █ ^ █ ║
║ ╬ ║ X ║
║ ╬ ║ X ║
║ # ║ # ║

Advantages And Disadvantages

The basic advantage of this design is that it uses much less water than infinite flow gates. A river is enough to supply even the more complex systems, maybe with an added reservoir to neutralise flow irregularities. Similarly, for the drain, it is enough to excavate a cavern where the water can evaporate.

The disadvantage is that it requires much more resources and time to construct, especially more mechanisms. And more planning, since floodgates tend to block paths when constructed.

Retrieved from "https://dwarffortresswiki.org/index.php?title=40d:Fluid_logic&oldid=58890"